Bipartite Graph Loopy Belief Propagation

In this document, we demonstrate a bipartite graph inference using loopy belief propagation. This experiment serves as a proof-of-concept for future implementation of large scale graph-based inference.

%matplotlib inline import opengm import matplotlib.pyplot as plt import matplotlib.cm as cm import numpy as np import Image import networkx as nx from networkx.algorithms import bipartite

Basic Setup

1. A bipartite graph \(G=(V,E)\) , where the vertices are partitioned into two groups: \(V=V_0\cup V_1\) , \(V_0\cap V_1=\emptyset\) ; the sets \(V_0\) , \(V_1\) are totally disconnected.
2. Each vertex stands for a Bernoulli random variable, and each edge represents a factor. Therefore, the scope of any factor contains exactly two vertices, one from each of \(V_0\) and \(V_1\) .
3. Initially, the marginal distribution of some of the random variables in \(V_0\) are known; all the rest of the marginal distributions are set to be uniform. The edge potentials (i.e., joint distributions determined by the factor) are set to be the tensor product of the marginal distributions of the two vertices linked by the edge.
4. Marginal distributions of some of the random variables associated with the vertices in \(V_0\) are known; all other marginals are assumed uniform. All messages are initialized as \(1\) .

A Toy Example

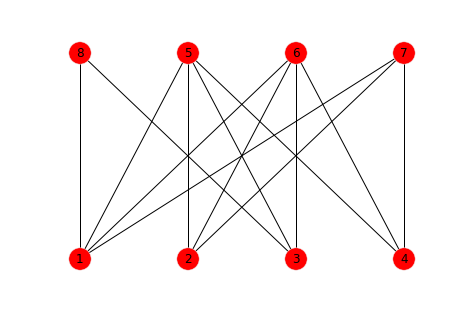
Consider the following bipartite graph

where nodes \(1\) , \(2\) , \(3\) , \(4\) each represents a domain, while \(5\) , \(6\) , \(7\) , \(8\) each stands for a property of the domain (e.g., certain registrant name, phone number, address, etc.). We assume the counts of infringing (denoted as \(I\) ) and non-infringing (denoted as \(N\) ) are known for only domains \(1\) , \(2\) ; marginal probability distributions for nodes \(3\) , \(4\) to generate infringing websites are to be inferred. Along the way, we shall also obtain the marginal probability distribution for property nodes \(5\) , \(6\) , \(7\) , \(8\) to produce infringing websites.

The \(I\) vs. \(N\) counts for nodes \(1,2\) are listed in the following table.

In this toy example, node \(1\) is connected to \(5,6,7,8\) , while node \(2\) is only connected to \(5,6,7\) . Note that node \(1\) is much more likely to generate infringing websites compared to node \(2\) ; it is reasonable to conjecture that this biase results from the connectivity between node \(1\) and node \(8\) . Among the nodes whose marginal probability distributions are to be inferred, node \(3\) connects to node \(8\) but node \(4\) doesn't. We thus expect a higher probability of generating infringing websites for node \(3\) than node \(4\) . In fact, since \(4\) connects to exactly the same properties as node \(2\) , we expect the marginal prbability distributions of node \(4\) to be close to those of node \(2\) .

We assume each node \(j\) is assigned a Bernoulli random variable \(X_j\) ( \(1\leq j\leq 8\) ). The potential functions on each node represents the prior belief for the corresponding random variable, estimated from the data if possible:

\begin \phi_1\left(I\right)=0.50, &\quad \phi_1\left(N\right)=0.50,\\ \phi_2\left(I\right)=0.85, &\quad \phi_2\left(N\right)=0.15,\\ \phi_3\left(I\right)=0.52, &\quad \phi_3\left(N\right)=0.48,\\ \phi_4\left(I\right)=0.50, &\quad \phi_4\left(N\right)=0.50. \end

Potential functions at each property node:

\begin \phi_5\left(I\right)=\frac=0.685, &\quad \phi_5\left(N\right)=0.315,\\ \phi_6\left(I\right)=\frac=0.685, &\quad \phi_6\left(N\right)=0.315,\\ \phi_7\left(I\right)=\frac=0.685, &\quad \phi_7\left(N\right)=0.315,\\ \phi_8\left(I\right)=\frac=0.85, &\quad \phi_8\left(N\right)=0.15. \end

On each edge we need to specify the conditional probability of a domain node producing an infringing website given the state of the propety node. We assume there is a constant probability \(\beta\in\left[0,1\right]\) for the domain node to behave the same way as the property node, e.g.,

\left(X_1=I\mid X_5=I\right)=\beta,\quad \mathbb

\left(X_1=I\mid X_5=N\right)=1-\beta,$$

\left(X_1=N\mid X_5=N\right)=\beta,\quad \mathbb

\left(X_1=N\mid X_5=I\right)=1-\beta.$$

Let us construct the graph in OpenGM . Click here for a user/developer manual.

numVar = 8 numLabels = 2 beta = 0.75 numberOfStates = np.ones(numVar, dtype=opengm.index_type)*numLabels gm = opengm.graphicalModel(numberOfStates, operator="multiplier") Edges = np.array([(1,5), (1,6), (1,7), (1,8), (1,6), (2,5), (2,6), (2,7), (3,8), (3,5), (3,6), (4,5), (4,6), (4,7)]) DomainNodes = set(Edges[:,0]) PropertyNodes = set(Edges[:,1]) DomainNodeCounts = np.array([[85,15],[52,48],[0,0],[0,0]]) # DomainNodeCounts = np.array([[99,1],[0,100],[0,0],[0,0]]) PropertyNodeCounts = [] for p in xrange(len(PropertyNodes)): PropertyNodeCounts.append([0.0, 0.0]) for v in Edges[Edges[:,1] == (p+1+len(DomainNodes)),:][:,0]: PropertyNodeCounts[p] += DomainNodeCounts[v-1] unaries = np.vstack([DomainNodeCounts, np.array(PropertyNodeCounts)]) for x in xrange(unaries.shape[0]): if (sum(unaries[x]) == 0.0) : unaries[x] = np.array(np.ones(numLabels) / sum(np.ones(numLabels))) else: unaries[x] = np.array(unaries[x] / sum(unaries[x])) for r in xrange(unaries.shape[0]): fid = gm.addFunction(unaries[r]) gm.addFactor(fid, r) for c in xrange(Edges.shape[0]): fid = gm.addFunction(np.array([[beta, 1-beta], [1-beta, beta]])) gm.addFactor(fid, np.array(Edges[c]-1, dtype=opengm.index_type))

Visualize the factor graph corresponding to the graphical model. Note that in the graphical model the node subindex starts with \(0\) .

opengm.visualizeGm(gm,show=False,layout="neato",plotUnaries=True, iterations=1000,plotFunctions=False, plotNonShared=False,relNodeSize=1.0) get node position. . done

inferBipartite = opengm.inference.BeliefPropagation(gm,parameter=opengm.InfParam(damping=0.01,steps=100), accumulator="integrator") inferBipartite.infer() print "Marginal Probabilities for Domain Nodes:" print "++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++" for d in xrange(4): print "Node generates infringing websites with probability ".format(d+1, inferBipartite.marginals(d)[0][0]) print "++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++" print "" print "Marginal Probabilities for Property Nodes:" print "++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++" for d in xrange(4): print "Node generates infringing websites with probability ".format(d+5, inferBipartite.marginals(d+4)[0][0]) print "++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++" Marginal Probabilities for Domain Nodes: ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Node 1 generates infringing websites with probability 0.921084363355 Node 2 generates infringing websites with probability 0.612357558773 Node 3 generates infringing websites with probability 0.621324912368 Node 4 generates infringing websites with probability 0.593463184578 ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Marginal Probabilities for Property Nodes: ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Node 5 generates infringing websites with probability 0.742725289156 Node 6 generates infringing websites with probability 0.826792875427 Node 7 generates infringing websites with probability 0.740086302281 Node 8 generates infringing websites with probability 0.878739154843 ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

As we expected, the model predicts higher infringing probability for Node \(3\) than Node \(4\) ; Node \(8\) has the highest probability of generating infringing websites among all property nodes.

Appendix: Loopy Belief Propagation (LBP)

1. Constructing the Cluster Graph

The first step in LBP is to construct a cluster graph from the orignal graph. This derived graph is undirected, with each node representing a cluster \(C_j\subset V\) . Let us denote the number of random varaibles in \(C_j\) as \(\left|C_j\right|\) . When \(C_j\cap C_k\neq \emptyset\) , define a sepset \(S_\subset C_j\cap C_k\) . Obviously, \(S_=S_\) .

Each factor \(\phi_k\) is assigned to a unique cluster \(C_<\alpha\left(k\right)>\) in the cluster graph. This assignment should at least ensure that \(\mathrm\left[\phi_k\right]\subset C_<\alpha\left(k\right)>\) . We then construct potentials for each cluster by

Some clusters may have more than one factors assigned to them, while other clusters may have none. In the latter case, initialize the corresponding potential to be \(1\) (one can assign a uniform distribution as well, but for potentials this doesn't matter --- the results will be renormalized to get a probability distribution).

Cluster graphs are generally non-unique.

2. Message Passing

The message passed from cluster \(C_i\) to \(C_j\) is

\psi_i\left(C_i\right)\prod_>m_\left(S_\right).$$

For each pair of subscripts \((i,j)\) , this formula translates into \(2^<\left|S_\right|>\) equalities. The summation involves \(2^<\left|C_i\backslash S_\right|>\) terms while the product combines \(2^<\left|N_i\right|-1>\) .

This process is repeated until two messages (one for each direction) are computed for each edge.

3. Summarize Beliefs

$$\beta_i\left(C_i\right)=\psi_i\left(C_i\right)\prod_m_\left(S_\right).$$

Note that this is a total number of \(2^<\left|C_i\right|>\) equalities.

useful links

• Department of Mathematics
• Math Everywhere @ Duke
• Wolfram Alpha

social

Proudly powered by Pelican, which takes great advantage of Python. -->

Powered by Pelican
last modified: